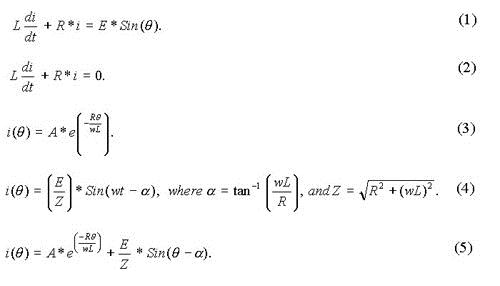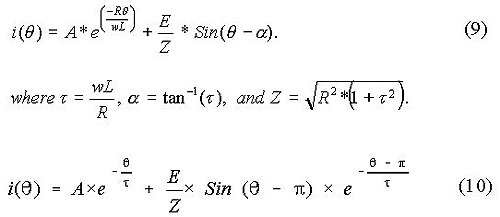Abstract

One of the first and most widely used application of power electronic devices have been in rectification. Rectification refers to the process of converting an ac voltage or current source to dc voltage and current. Rectifiers specially refer to power electronic converters where the electrical power flows from the ac side to the dc side. In many situations the same converter circuit may carry electrical power from the dc side to the ac side where upon they are referred to as inverters. We will be Designing and Simulating single phase half wave Rectifier; commonly used rectifier circuits supplying different types of loads (resistive, inductive, capacitive, back emf type) will be presented.

Contents

• Introduction……………………………………………
• Objectives of the Project…………………………..
• Point of interests
• Circuit Description & Operation………………..
• Mathematical Analysis…………………………….
• Computer simulation
  • Software Code
  • Sample Run
  • Outputs
    • Circuit
    • Outputs
    • Block Diagram
    • Outputs

1.      MATLAB Simulation

2.      MATLAB Simulink (Time Domain Implementation)

3.      MATLAB Simulink (Frequency Domain Implementation)

4.      Multisim Implementation…………………………

 

Introduction

Single phase rectifiers are extensively used in a number of power electronic based converters. In most cases they are used to provide an intermediate unregulated dc voltage source which is further processed to obtain a regulated dc or ac output. They have, in general, been proved to be efficient.

 

Objectives of the Project:

• Analyze the operation of single phase half wave rectifier supply resistive, inductive loads.
• Define and calculate the Performance Parameters of the rectifier.
• Simulate the circuit with computer software package (MATLAB)
• In addition to MATLAB we also simulated the project in Multisim

 

Points of interest in the analysis will be.

•   Waveforms and characteristic values (average, RMS etc) of the rectified voltage and current.

•   Influence of the load type on the rectified voltage and current.

•   Reaction of the rectifier circuit upon the ac network, reactive power requirement, power factor, harmonics etc.

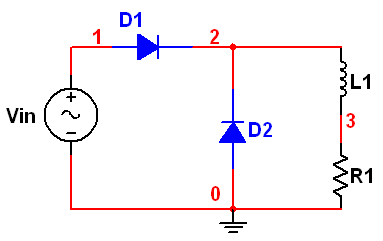
Circuit Description & Operation:

Let the source voltage v_s be defined to be E*sin (wt). The source voltage is positive when 0 < wt < pi  radians and it is negative when pi < wt < 2 pi radians. When v_s is positive, diode D₁ conducts and the voltage v_c is positive. This in turn leads to diode D₂ being reverse-biased during this period. During  pi < wt < 2 pi the voltage v_c would be negative if diode D₁ tends to conduct. This means that D₂ would be forward-biased and would conduct. When diode D₂ conducts, the voltage v_c would be zero volts, assuming that the diode drop is negligible. Additionally when diode D₂ conducts, diode D₁ remains reverse-biased, because the voltage v_s is negative. When the current through the inductor tends to fall, it starts acting as a source. When the inductor acts as a source, its voltage tends to forward bias diode D₂ if the source voltage v_s is negative and forward bias diode D₁ if the source voltage v_s is positive. Even when the source voltage v_s is positive, the inductor current would tend to fall if the source voltage is less than the voltage drop across the load resistor. During the negative half-cycle of source voltage, diode D₁ blocks conduction and diode D₂ is forced to conduct. Since diode D₂ allows the inductor current circulate through L, R and D₂, diode D₂ is called the free-wheeling diode. We can say that the current free-wheels through D₂.

Mathematical Analysis

An expression for the current through the load can be obtained as shown below. It can be assumed that the load current flows all the time. In other words, the load current is continuous. When diode D₁ conducts, the driving function for the differential equation is the sinusoidal function defining the source voltage. During the period defined by pi < wt < 2pi, diode D₁ blocks current and acts as an open switch. On the other hand, diode D₂ conducts during this period, the driving function can be set to be zero volts. For 0 < wt <pi, the equation (1) shown below applies.

For the negative half-cycle of the source, equation (2) applies. As in the previous case, the solution is obtained in two parts. The expressions for the complementary integral and the particular integral are the same. The expression for the complementary integral is presented by equation (3). The particular solution to the equation (1) is the steady-state response and is presented as equation (4). The total solution is the sum of both the complimentary and the particular solution. The total solution is presented as equation (5).

The difference in solution is in how the constant A in complementary integral is evaluated. In the case of the circuit without free-wheeling diode, i(0) = 0, since the current starts building up from zero at the start of every positive half-cycle. On the other hand, the current-flow is continuous when the circuit contains a free-wheeling diode also. Since the input to the RL circuit is a periodic half-sinusoid function, we expect that the response of the circuit should also be periodic. That means, the current through the load is periodic. It means that i(0) = i(2).

Since the current through the load free-wheels during  <  < 2, we get equation (6). We use ( -  ) for the elapsed period in radians instead of  itself, since the free-wheeling action starts at  =  . From the total solution, we can get i() from equation (7) by substituting  = . To obtain A, the following steps are necessary. From the total solution, obtain an expression for i(0) by substituting 0 for . Also obtain an expression for i() by substituting  for in equation (7). Using this expression for i() in equation (6), obtain i(2) by letting  = 2 . Since i(0) = i(2), we can obtain A from equation (8). In equation (8), the terms containing constant A are grouped on the left-hand side of equation and the other terms on the right-hand side.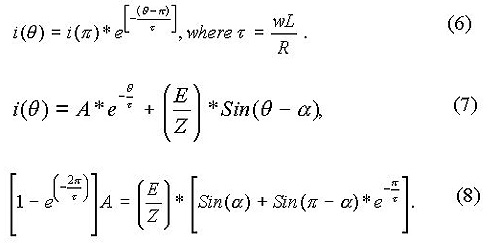

The operation of the circuit can be simulated as shown below. During 0 <  <  , the expression for current is presented as equation (9). During  <  < 2 , the expression for current is shown as equation (10).

Computer simulation

We simulated the project using various computer simulation techniques, the soft form is also provided

MATLAB Simulation

Software Code:

%PROJECT TITLE:

%DESIGN AND IMPLEMENTATION OF HALF WAVE RECTIFIER

disp(‘%%%%%%%%%%%%%%%%%% POWER ELECTRONICS PROJECT %%%%%%%%%%%%%%%%%%%%%’);

disp(‘%%%%%%%%%%%%%%%%% DESIGN AND IMPLEMENTATION OF %%%%%%%%%%%%%%%%%%%’);

disp(‘%%%%%%%%%%%%%%% SINGLE PHASE HALF WAVE RECTIFIER %%%%%%%%%%%%%%%%%’);

disp(‘%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%’);

disp(‘%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%’);

disp(‘%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%’);

disp(‘%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%’);

disp(‘ENTER REQUIRED DESIGN PARAMETERS…’)

%PEAK VOLTAGE: Vp IN VOLTS

peakV=input(‘ENTER PEAK VOLTAGE IN VOLTS: ‘);

%CIRCUIT OPERATI0N FREQUENCY freq (Hz)

freq=input(‘ENTER OPERATING FREQUENCY IN Hz: ‘);

%LOAD INDUCTANCE L(mH)

L=input(‘ENTER LOAD INDUCTANCE IN mH: ‘);

%LOAD RESISTANCE R(Ohms)

R=input(‘ENTER LOAD RESISTANCE IN ohm: ‘);

%Setting the required parameters

w=2.0*pi*freq;

angle=atan(w*L/R);

Idc =0.318*peakV/R;

Vdc=0.318*peakV;

X=w*L/1000.0;

if (X<0.001) X=0.001; end;

Z=sqrt(R*R+X*X);

tauInv=R/X;

loadAng=atan(X/R);

A1=peakV/Z*sin(loadAng);

A2=peakV/Z*sin(pi-loadAng)*exp(-pi*tauInv);

A3=(A1+A2)/(1-exp(-2.0*pi*tauInv));

Ampavg=0;

AmpRMS=0;

dccur =0;

dcvolt=0;

Pdc = 0;

for n=1:360;

theta=n/180.0*pi;

X(n)=n;

if (n<180)

cur=peakV/Z*sin(theta-loadAng)+A3*exp(-tauInv*theta);

Ampavg=Ampavg+cur*1/360;

AmpRMS=AmpRMS+cur*cur*1/360;

else

A4=peakV/Z*sin(pi-loadAng)*exp(-(theta-pi)*tauInv);

cur=A4+A3*exp(-tauInv*theta);

Ampavg=Ampavg+cur*1/360;

AmpRMS=AmpRMS+cur*cur*1/360;

end;

if (n<180)

Vind(n)=peakV*sin(theta)-R*cur;

Vout(n)=peakV*sin(theta);

diode2cur(n)=0;

diode1cur(n)=cur;

dcvolt = sqrt(Vout(n))/2;

else

Vind(n)=-R*cur;

Vout(n)=0;

diode2cur(n)=cur;

diode1cur(n)=0;

end

Vrms=peakV/2;

Irms=Vrms/R;

Is1=Irms;

iLoad(n)=cur;

dccur = sqrt(iLoad(n))/2;

end;

disp(‘SINGLE PHASE HALF WAVE RECTIFIER PERFORMANCE PARAMETERS’);

Pdc = Vdc*Idc;

disp(‘1: The Average DC Power is…’);

disp(Pdc);

Pac = Vrms*Irms;

disp(‘2: The Average AC Power is…’);

disp(Pac);

eff=Pdc/Pac;

disp(‘3: THE PERCENTAGE RECTIFICATION RATIO OF THE RECTIFIER…’);

disp(eff);

Vac=sqrt(Vrms^2-Vdc^2);

disp(‘4: The Effective Value Of AC Componenet of Output Voltage is…’);

disp(Vac);

FF=Vrms/Vdc;

disp(‘5: The Form Factor is…’);

disp(FF);

RF=Vac/Vdc;

disp(‘6: The Ripple Factor is…’);

disp(RF);

TUF=Pdc/(Vrms*Irms);

disp(‘7: The Transformer Utilization Factor is…’);

disp(TUF);

DF=cos(angle);

disp(‘8: The Displacement Factor is…’);

disp(DF);

HF=sqrt((Irms/Is1)-1);

disp(‘9: The Harmonic Factor is…’);

disp(HF);

PF=(Is1/Irms)*cos(angle);

disp(’10: The Power Factor is…’);

disp(PF);

CF=peakV/(R*Irms);

disp(’11: The Crest Factor is…’);

disp(CF);

%Plotting Corresponding input and Output Currents and Voltages

plot(X,iLoad,’m’)

title(‘The Load current’)

xlabel(‘degrees’)

ylabel(‘Amps’)

grid

pause

plot(X,Vout,’r’)

title(‘Voltage at cathode’)

xlabel(‘degrees’)

ylabel(‘Volts’)

grid

pause

plot(X,Vind,’b’)

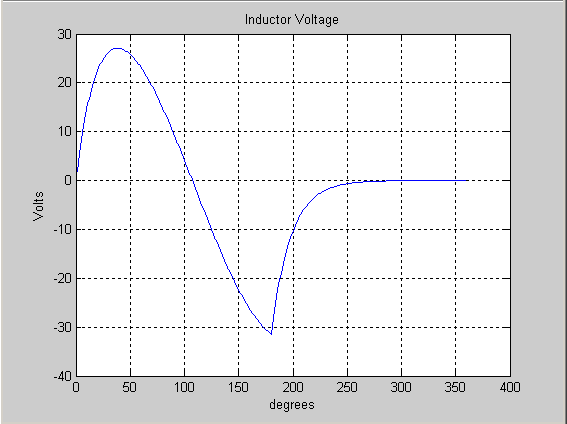
title(‘Inductor Voltage’)

xlabel(‘degrees’)

ylabel(‘Volts’)

grid

pause

plot(X,diode1cur,’m’)

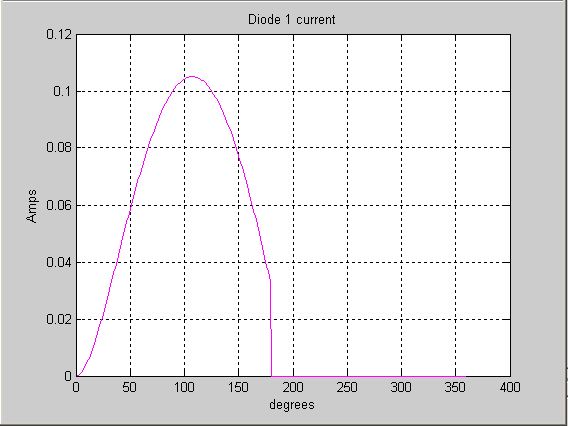
title(‘Diode 1 current’)

xlabel(‘degrees’)

ylabel(‘Amps’)

grid

pause

plot(X,diode2cur,’r’)

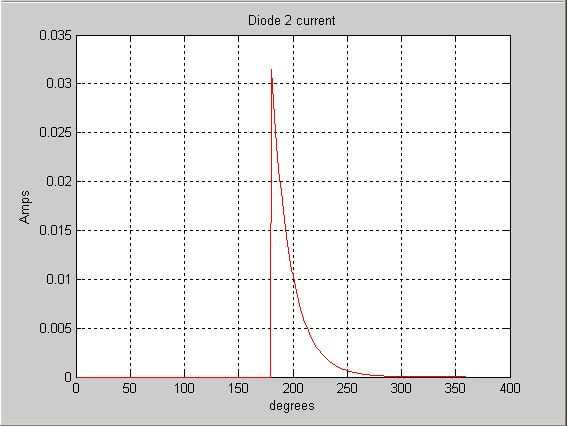
title(‘Diode 2 current’)

xlabel(‘degrees’)

ylabel(‘Amps’)

grid

Sample Run:

%%%%%%%%%%%%%%% POWER ELECTRONICS PROJECT %%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%% DESIGN AND IMPLEMENTATION OF %%%%%%%%%%%%%%%

%%%%%%%%%%%%% SINGLE PHASE HALF WAVE RECTIFIER %%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

ENTER REQUIRED DESIGN PARAMETERS…

ENTER PEAK VOLTAGE IN VOLTS: 110

ENTER OPERATING FREQUENCY IN Hz: 50

ENTER LOAD INDUCTANCE IN mH: 1000

ENTER LOAD RESISTANCE IN ohm: 1000

 

%%%%%%%%%%%%%%%%%%%%%%%%%%% OUTPUT %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

SINGLE PHASE HALF WAVE CONTROLLED RECTIFIER PERFORMANCE PARAMETERS

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

1: The Average DC Power is…

1.2236

 

2: The Average AC Power is…

3.0250

 

3: The Efficiency Of Rectifier is…

0.4045

 

4: The Effective Value Of AC Componenet of Output Voltage is…

42.4429

 

5: The Form Factor is…

1.5723

 

6: The Ripple Factor is…

1.2133

 

7: The Transformer Utilization Factor is…

0.4045

 

8: The Displacement Factor is…

0.0032

 

9: The Harmonic Factor is…

0

 

10: The Power Factor is…

0.0032

 

11: The Crest Factor is…

2

 

OUTPUTS:

The Voltage waveform at output or at the cathodes of both the diodes:

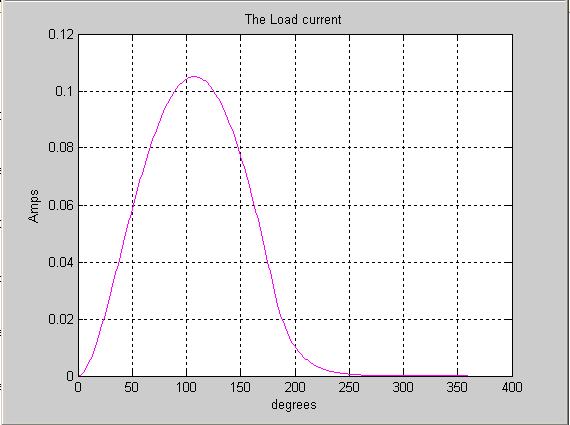
The current waveform at output or Load current:

The voltage waveform across the inductor:

Diode1 current waveform:

Diode2 current waveform:

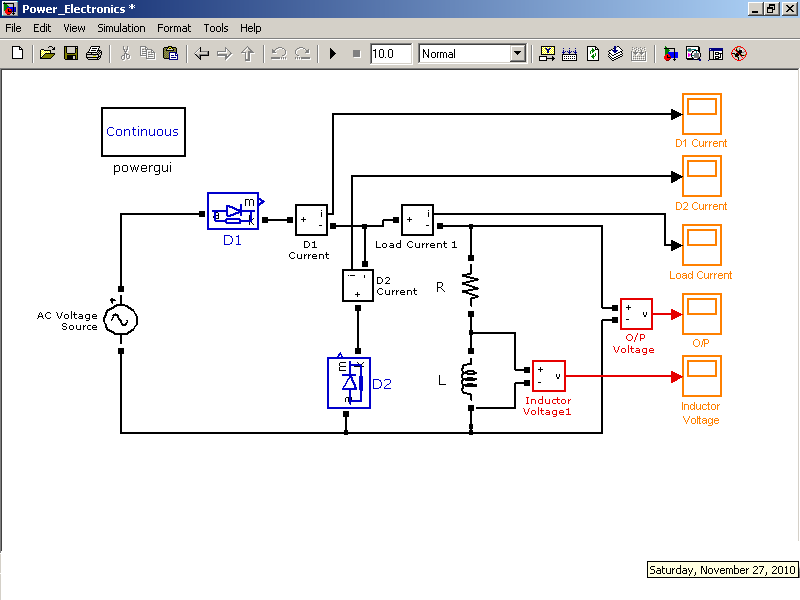
MATLAB Simulink (Time Domain Implementation)

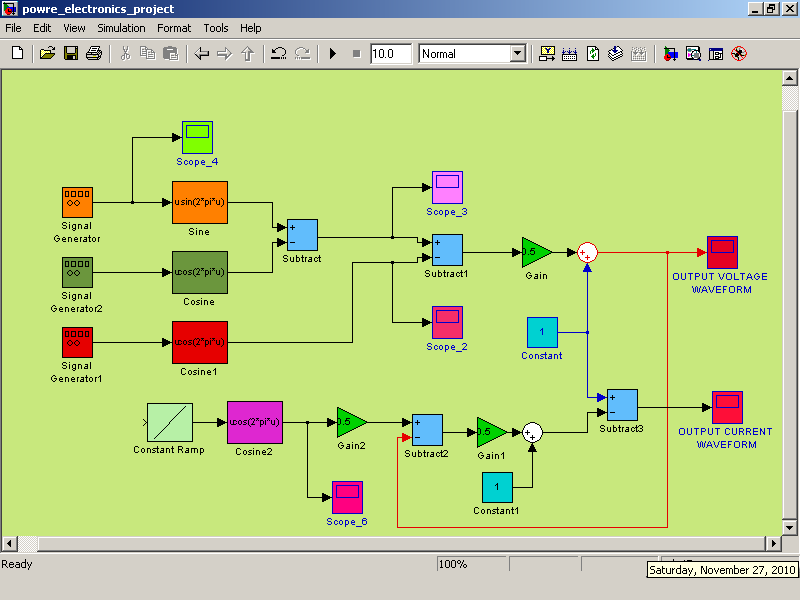
Following is the Matlab Simulink Implementation in time domain:

 

OUTPUTS:

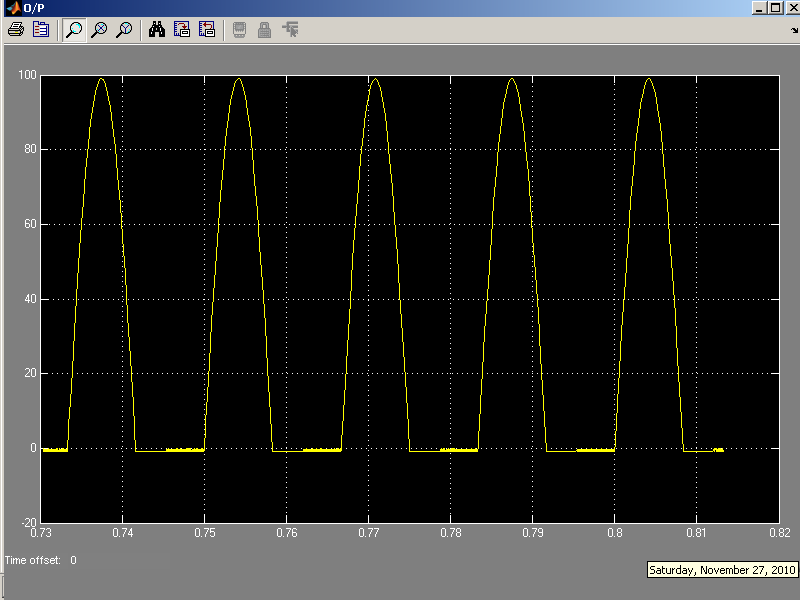
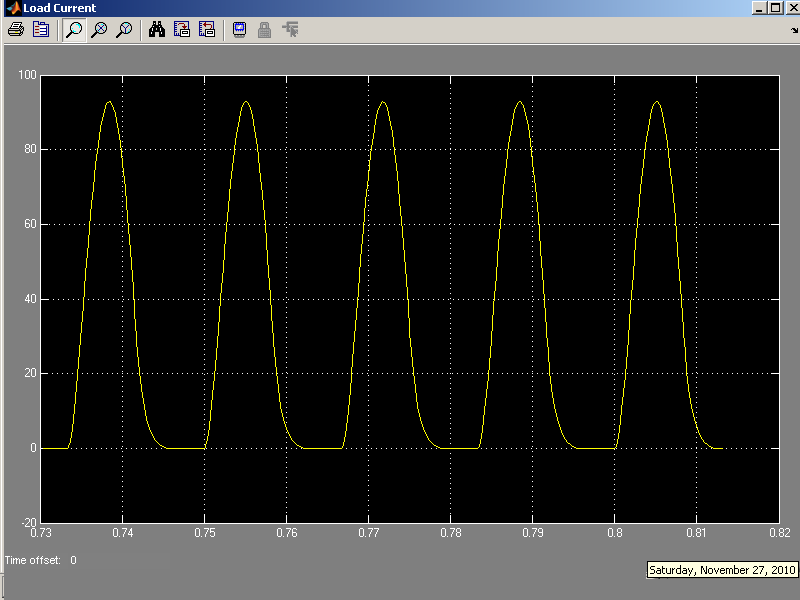
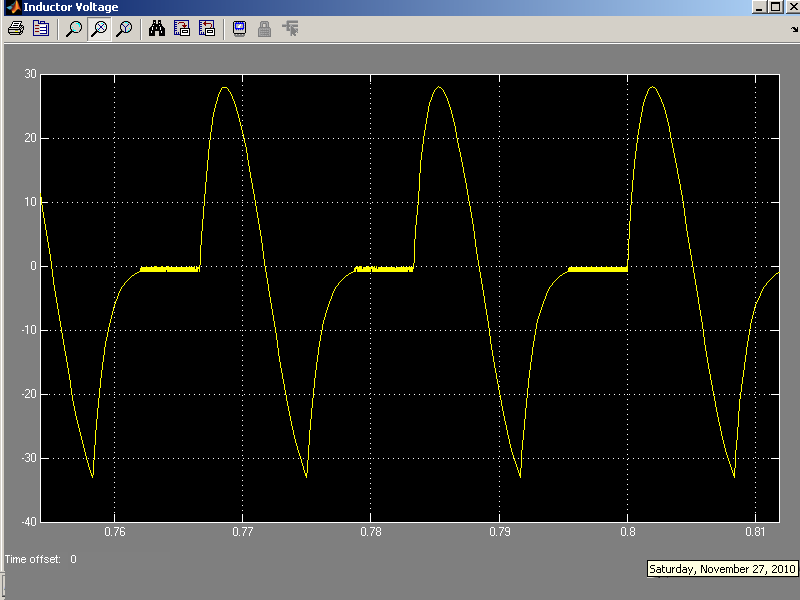
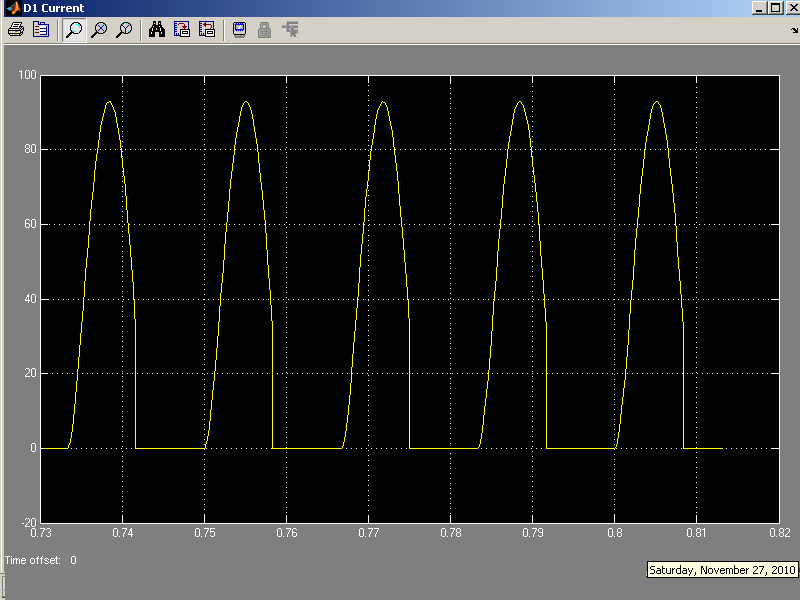
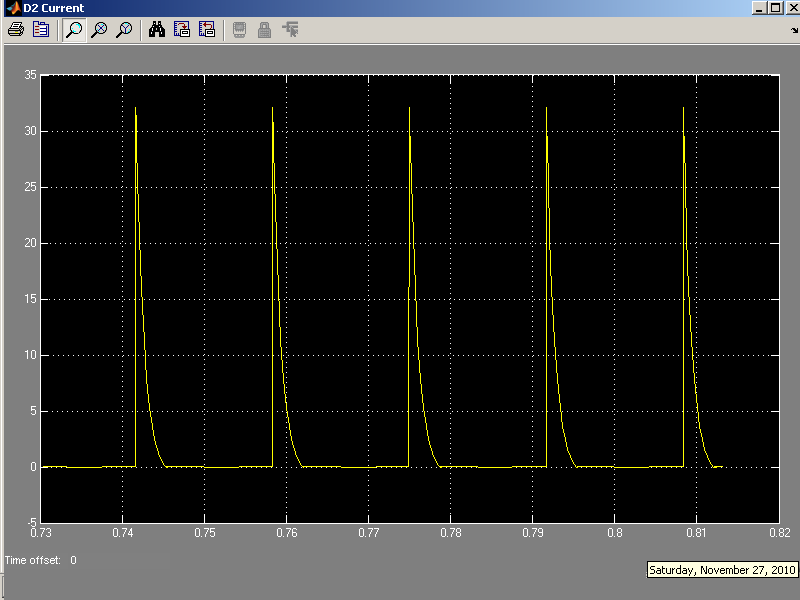
MATLAB Simulink(Frequency Domain)

Following is the Matlab Simulink Implementation in Frequency domain:

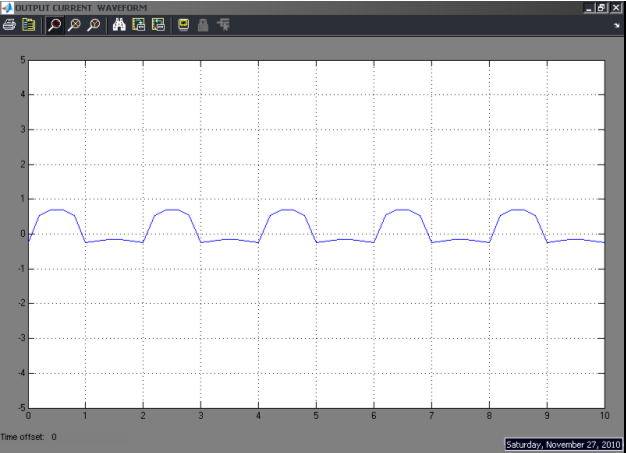
MULTISIM Implementation:

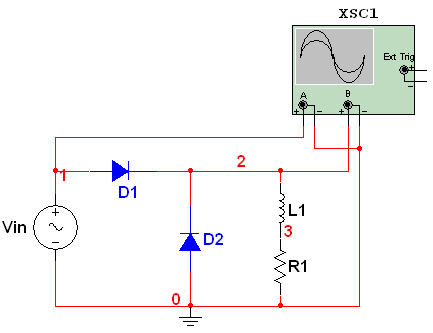
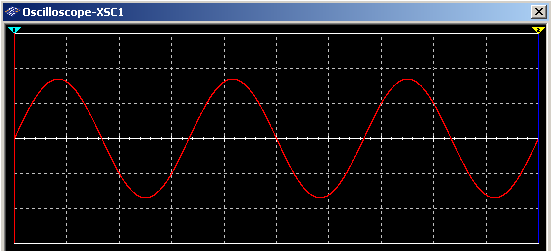
The waveform of voltage at the Input

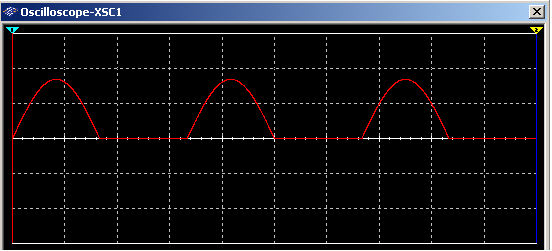
The waveform of voltage at the cathode of both diodes i.e. Output voltage

 

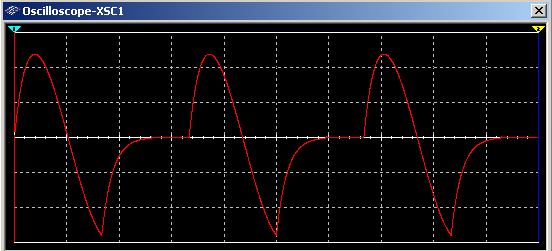
The waveform of voltage across the inductor