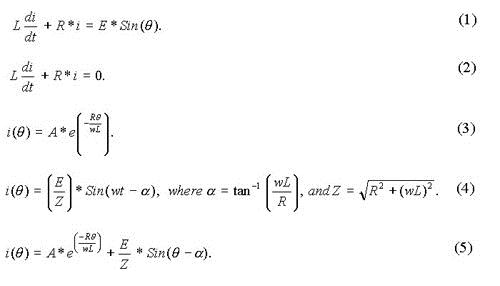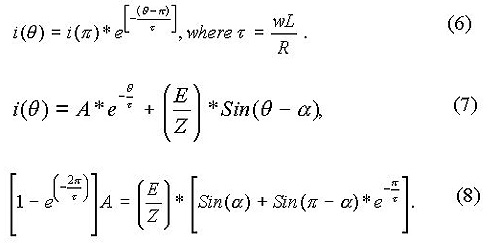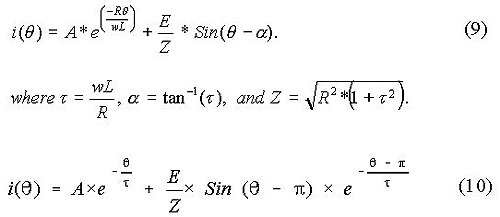Every year GIKI offers admissions in Undergraduate Engineering programs. Here we will provide info about GIKI Undergraduate Admissions 2013 including prospectus, application process, GIKI Entry Test 2013, GIKI undergraduate merit lists and all other aspects of admission. Note that we are only facilitating students with the admission information, all the admission process will be dealt with the University itself. Thousands of intermediate students from all over the Pakistan apply for admissions every year in undergraduate engineering programs of Ghulam Ishaq Khan Institute. GIKI is one of the top most engineering institute of Pakistan.
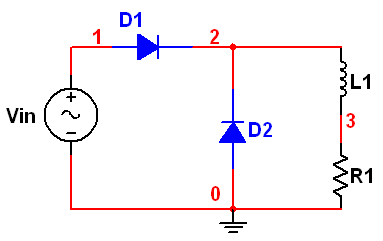
GIKI Admissions 2013 Procedure Overview
GIKI announces its undergraduate admissions in April or May of every year. This year the admission process will start from 28th April 2013 with the availability of Prospectus. Then the online form submission for admissions will start from 28th April 2013. The last date for the admission submission is 20th June 2013. After the last date of form submission GIKI will provide the admit cards for the Admission test (GIKI Entry Test 2013). The entry test will held on 7th July 2013. After that Admission test result will be announced and merit lists will be displayed. The admitted candidates will then start their first semester on 26th August 2013.
GIKI Application Procedure
- Create an account (register yourself) . https://admission.giki.edu.pk
- Login and submit online application form
- Prepare a package of the following documents:
- Admit Card (printed online)
- Application Form (printed online)
- Optional Scholarship Form (printed online)
- Proof of payment: Rs. 2500 (for local) + Rs. 500 (if applying for financial assistance) / US $170 (overseas)
- Photocopies of Academic Documents
- Two additional passport size photographs
- Send the above documents (in Single package) at the address given as below:
Undergraduate Admission Office
GIK Institute of Engineering Sciences & Technology
Khyber Pakhtunkwa, Pakistan
Ph: +92-938-271440
Cell: +92-334-8696119
- How to pay the Application Processing fee ?
Processing fee can be paid:
Online to HBL A/C No. 19790000085901 for payment in PKR
OR
For payment in US $:
Bank: Habib Bank Ltd
Title of Account: GIK Institute Topi
Account No: 19790002044611
Branch Code: 1979
Swift Code: HABB PKK AXXX
- To send your SAT-II Score, use GIK Institute’s registered Institute Code: 0096
GIKI UG Admission Schedule
|
Event |
Date |
|
Availability of Prospectus – Class of 2017 |
Apr 28, 2013 |
|
Online Submission of Admission Form Starts |
Apr 28, 2013 |
|
Online Submission of Admission Form Ends |
Jun 20, 2013 |
|
Last date for receipt of documents |
Jun 23, 2013 |
|
Admission Test |
Jul 07, 2013 |
|
Last date for receipt of SAT- II Scores (overseas applicants) |
Jul 08, 2013 |
|
Induction Ceremony |
Aug 24, 2013 |
|
Semester Starts |
Aug 26, 2013 |
GIKI Entry Test 2013
GIKI offers admissions on the basis of candidate’s earlier academic background and the score of the Admission test conducted by GIKI. This admission test is also known as GIKI Entry Test. This admission test is very important and the admission of the candidate mostky depends on the score of this admission test. the weight-age of this admission test in the selection process is 85%. For more information about the GIKI Entry test and its pattern and sample test paper, visit the link given below.
Click GIKI Entry Test 2013 for details
Click GIKI Entry Test Result 2013 to check result
Undergraduate Programs
GIKI offers admissions in the following undergraduate programs:
- Computer Science and Engineering
- Electronic Engineering
- Chemical Engineering (Newly announced Undergraduate program)
- Electrical Engineering (Power) (Newly announced Undergraduate program)
- Engineering Sciences
- Humanities & Management Sciences
- Mechanical Engineering
- Metallurgy & Materials Engineering/ Material Science and Engineering
- Mathematics
- Physics
- Bachelor in Management Sciences (Newly announced Undergraduate program)
Basic Eligibility Criteria
| Basic Eligibility for Engineering and Computer Science Programs |
1. HSSC (Pre-Engineering i.e Mathematics, Physics and Chemistry) 2. HSSC (Pre-Medical) with Additional Mathematics 3. Three A-level in Mathematics, Physics and Chemistry and O-level in eight subjects (English, Mathematics, Physics, Chemistry, Biology/Computer Science, Urdu, Islamic Studies & Pakistan Studies) for local applicants and in five required subjects for those applying from abroad. 4. American or Canadian High School Diploma or International Baccalaureate Diploma with Mathematics (with Calculus), Physics and Chemistry 5. B.Sc. (Mathematics & Physics) 6. Three year Diploma of Associate Engineering (DAE) in relevant technology from a Pakistani Board of Technical Education |
60% marks or Equivalent Grades in Mathematics, Physics and Overall |
| Note: Applicant with Mathematics, Physics and Chemistry background can apply for all programs however those having studied Computer Science / Computer Studies in lieu of Chemistry at their HSSC or A-levels, can only apply for Computer Engineering or Computer Science. | ||
| Basic Eligibility Management Science Program |
1. HSSC (Pre-Engg), HSSC (General Science), HSSC (ICS), HSSC (Pre-Medical) with Additional Mathematics 2. A-Level in three subjects and O-Level in eight subjects for local OR O-Level in five subjects for those applying from abroad 3. American or Canadian High School Diploma or International Baccalaureate Diploma
|
60% Marks or Equivalent grades |
| Comparative Assessment (Merit List) | CriterionScore in Admission Test OR SAT II in Mathematics and Physics for those applying from outside Pakistan (For Engineering and Computer Science Programs)Score in GCAT (GIKI Common Admission Test) OR SAT for those applying from outside Pakistan (For Management Science Program)
SSC/Equivalent + HSSC Part I O-level (for those with A- and O-level background) Last completed qualification for IB diploma or B.Sc. or DAE |
Weightage85%
85%
5% + 10% 15% 15% |
GIKI UG Admissions Contact Info
Phone No. NWD : 0938-271440
Cell # 0334-8696119, 0303-5394528
Email: [email protected]
Further information about the GIKI Admissions 2013 will be updated soon. The eligibility criteria, selection procedure, Scholarship and loans information will be avialable soon, so stay with us and keep visiting us. We will keep you up to date with the GIKI admission process.
If students have any queries regarding GIKI admissions, they can ask us by commenting below in the comment section. We will utterly try to help them. Don;t forget to share this admission news with your friends; you can share this by clicking the sharing buttons given below.
Click Engineering Admissions 2013 for other university’s admissions